Mathematik für Mathematik-Muffel

Wenn Schüler heute mit kariertem Schulheft, Geodreieck und Zirkel über die Konstruktion geometrischer Formen grübeln, dann stehen sie in einer Tradition, die weit ins Mittelalter zurückreicht: Schon in den Klosterschulen gehörte die Geometrie Euklids zum Lehrplan.

Artikeltext:

Wie vermittelt man die Grundlagen der Geometrie?

Wir kennen heute den „Lehrplan“, den alle Klosterschüler durchliefen, als die sieben freien Künste: Grammatik, Rhetorik und Dialektik in der Grundstufe, Arithmetik, Geometrie, Musik und Astronomie in der Oberstufe. Dieser Wissenskanon galt bis weit in die frühe Neuzeit als verbindlich. Er war die Grundlage für jeden Studenten, der sich an einer Universität einschreiben wollte.

Das wichtigste Lehrbuch im Fach Geometrie stammte aus der Feder des griechischen Mathematikers Euklid. Seine „Elemente“ beherrschten das Fach bis zum Jahr 1830(!) derart, dass wir die Geometrie bis zur dritten Ebene - also Linie / Quadrat / Würfel - immer noch als euklidische Geometrie bezeichnen.

Dabei wissen wir über den historischen Euklid nicht allzu viel. Er dürfte um das 4./3. Jahrhundert v. Chr. am Museion im ägyptischen Alexandria gewirkt haben. Nicht einmal seine Lebensdaten stehen fest. Er könnte um 360 v. Chr. in Athen geboren worden sein und seine Ausbildung an Platons Akademie erhalten haben, oder er verfasste seine Werke erst um 300 v. Chr. und starb um 270 v. Chr.

Doch seine Lebensgeschichte ist für unsere Zwecke völlig irrelevant. Es ist sein Buch, die „Elemente“, das im Mittelalter Karriere machte. Es beschäftigt sich ausgehend vom Punkt mit der Konstruktion von Linien und Körpern und fasste damit das geometrische Basiswissen für jeden zusammen, der den Bauplan für eine Kirche entwerfen wollte. Quadrate und Kreise nebeneinander oder übereinander geschichtet waren Jahrhunderte lang die Formen, mit denen Baumeister Gebäude konstruierten. Deshalb standen die Elemente von Euklid in hohen Ehren. In jeder besseren Klosterbibliothek existierte mindestens eine Handschrift.

Was die Mathematik mit Gott verbindet

Nun lasen unsere Mönche mit der gleichen Begeisterung Euklid, mit der sie auch die Werke der antiken Kirchenväter rezipierten. Und die beschäftigten sich ebenfalls mit der Mathematik. Denn vieles übernahmen Augustinus & Co. von Platon und Pythagoras - ja, genau, von dem Philosophen, nach dem der bekannte Satz benannt wurde. Deshalb fand sowohl die Formel a²+b²=c² Eingang in die christliche Erziehung, als auch Platons Behauptung, dass die Geometrie zur „Erkenntnis des ewig Seienden“ führe. Platon sah in perfekten Kreisen und Quadraten das Göttliche, während er die keinen geometrischen Regeln unterliegenden Gegenstände der materiellen Welt für einen matten Abglanz vom Licht der gleißenden Ideen hielt.

Damit inspirierte er prachtvolle Kirchen, die nach streng geometrischen Regeln errichtet wurden. Der Kreis galt als Abbild des Himmels, als Symbol dafür, dass sich dieser um Gottvater drehe, genauso wie der Kreis um den Punkt gezogen wird. Das Quadrat dagegen stand für die Erde mit ihren vier Himmelsrichtungen. Wenn ein Architekt also mit Hilfe der bei Euklid gelernten Methoden die quadratische Vierung einer Kathedrale mit einer über einem Kreis konstruierten Kuppel überwölbte, dann war das die Stein gewordene Botschaft, dass der Gläubige von der irdischen Welt in den Himmel aufzusteigen in der Lage war.

Mathematik wird chic

Jahrhundertelang war die Geometrie für die Architekten existentiell und spielte trotzdem im Leben der anderen Menschen eine ähnlich unwichtige Rolle, wie sie es heute noch tut: Man lernt die Konstruktion eines gleichschenkligen Dreiecks in der Schule und vergisst sie dann so bald wie möglich. Welchen Grund gäbe es schon in einem normalen Durchschnittsleben, ein gleichschenkliges Dreieck zu konstruieren?

Doch dann adaptierte das Abendland irgendwann zwischen Spätmittelalter und Frührenaissance die arabischen Zahlen. Sie ermöglichten völlig neue Formen des Rechnens, und damit wurde die Mathematik auf einmal etwas, über das viele Intellektuelle sprachen und schrieben. Es war chic, in der Lage zu sein, schwierige mathematische Probleme zu lösen. Fürsten hielten sich begabte Mathematiker und begannen, sich selbst mit der Mathematik zu beschäftigten. Man unterhielt sich bei Gesellschaften und in Briefwechseln damit, dem Gegenüber ein möglichst kompliziertes mathematisches Problem vorzulegen, und dann demjenigen zu applaudieren, der es aufzulösen verstand. Humanisten und Künstler, die das Interesse eines Mäzens auf sich lenken wollten, taten also gut daran, zumindest die Grundzüge der Mathematik zu beherrschen.

Besonders hart dürfte die Konkurrenz um potente Mäzene zu Beginn des 15. Jahrhunderts in Florenz gewesen sein, wo eine Reihe von hervorragenden Künstlern um gut bezahlte Projekte buhlten. Einer von ihnen war Filippo Brunelleschi (1377-1446). Er verblüffte die Florentiner Kunstwelt im Jahr 1410 mit einer Attraktion: Er schuf ein perspektivisch korrektes Bild vom Baptisterium, indem er sich zum ersten Mal seit der Antike der Linearperspektive bediente. Ein Betrachter soll damals, wie uns Vasari überliefert, nicht in der Lage gewesen sein, einen Unterschied zwischen dem Spiegelbild des Baptisteriums und Brunelleschis gemaltem Bild zu finden.

Und was hat nun Euklid damit zu tun?

Die Inspiration zu seinem innovativen Bild verdankte Brunelleschi Euklids Werk mit dem Titel Optika (= Optik). Darin beschreibt der griechische Mathematiker seine Theorie über das Sehen. Es dreht sich um die Frage, wie ein Auge seine Umgebung wahrnimmt. Für Euklid senden alle Gegenstände Sichtstrahlen aus, die in Form eines Kegels auf das Auge treffen. Er formulierte seine Hypothese als ein geometrisches Problem, indem er die Einfallswinkel der Strahlen aufs Auge berechnete.

Sein Sichtkegel ist nach streng geometrischen Grundsätzen aufgebaut: Was näher ist, scheint uns wegen des engeren Sichtkegels größer, was weiter entfernt ist, wirkt kleiner. Euklid lieferte Brunelleschi mit seiner Schrift Optika die theoretischen Grundlagen dafür, auf Grund mathematischer Gesetze zu konstruieren, wie er das Baptisterium zeichnen müsse, um es trotz des flachen Untergrundes dreidimensional wirken zu lassen.

Euklids Optik, die Erfindung der Perspektive und ihre Anwendung

Das erste uns erhaltene Gemälde, das gemäß Euklids Linearperspektive konzipiert wurde, ist ein Fresko des Florentiner Künstlers Masaccio. Die Kassetten des Tonnengewölbes verkleinern sich systematisch entlang der Fluchtlinien von vorne nach hinten. Das Bild bringt die Perspektive ins Spiel. Generationen von Künstlern sollten sich an der Beherrschung der Perspektive abarbeiten und sie zu immer neuen Höhenflügen führen. Glanzpunkt dieser Entwicklung sind die Freskos des Rokoko. Meistern ihrer Kunst gelang es, mittels der virtuos angewandten Gesetze der Perspektive auf einer praktisch flachen Kirchendecke einen Blick in den nach oben offenen Himmel darzustellen.

Die Grundlage für all das, war Euklid. Durch ihn wurden Geometrie und Malerei zu zwei Seiten einer Münze. Nach Massacio kam kein Künstler, der für modern gelten wollte, um ausgedehnte mathematische Studien herum. Und das hatte für ihren Stand einen angenehmen Nebeneffekt: Vorbei waren die Zeiten, als die Malerei als reines Handwerk galt. Nun stand die Theorie im Mittelpunkt, und das mit allen sozialen Folgen. Der Künstler kletterte die gesellschaftliche Leiter nach oben. Es öffnete sich ihm der Zugang zum Fürstenhof. Er diskutierte als Gleichrangiger mit Humanisten, Politikern und Höflingen. Wobei gerade die Höflinge alles andere als erfreut waren über die neue Konkurrenz. 

Wie schwer sie den Eindringlingen das Leben machten, illustriert eine Anekdote aus dem Leben von Leonardo da Vinci: Er war zu Gast am Hof des Ludovico Sforza und forderte geradezu von ihm die Gelegenheit, im gelehrten Rededuell – ja, so etwas gab es damals, und es war richtig beliebt - seine Bildung zu zeigen. Im Februar des Jahres 1498 kamen alle Mitglieder des Hofes von Ludovico Sforza zusammen, um zu sehen, wie sich dieser uneheliche Sohn eines kleinen Advokaten aus Vinci gegen die hochlöblichen Adligen und studierten Doktoren der Universitäten schlagen würde. Natürlich ging Leonardo als Sieger aus diesem Rededuell hervor, auch weil er einen guten Mathematiklehrer gehabt hatte.

Sein Freund Luca Pacioli gehört nämlich zu den größten Mathematikern seiner Zeit. Von ihm lernte Leonardo da Vinci die Gesetze der Perspektive, die er in seinem späteren Leben so meisterhaft anwenden sollte. Die beiden Genies tauschten sich sowohl über Fragen der Kunst als auch über mathematische Probleme miteinander aus, und die gemeinsame Frucht ihrer Überlegungen floss in das 1509 veröffentlichte Buch „De divina proportione“ (= Über die göttlichen Verhältnisse) ein. Leonardo da Vinci illustrierte höchstpersönlich den von Luca Pacioli verfassten Text über den Goldenen Schnitt.

Dass die „Elemente“ des Euklid mit ihrer Grundlagenforschung zur Geometrie für Pacioli „elementar“ war, bringt ein 1495 entstandenes Porträt auf den Punkt: Die Hand des genialen Mathematikers ruht beim Entwerfen einer geometrischen Figur auf den Schriften Euklids.

Der Basler Euklid

Bald sprachen nicht mehr nur die italienischen Künstler über die Bedeutung von Euklid. Seine Werke wurden auch jenseits der Alpen zur Pflichtlektüre. Albrecht Dürer war ein wichtiges Glied in der Kette des Wissenstransfers. Ihm wird der zweite Teil unseres Essays „Mathematik: Die Königin der Wissenschaft“ gewidmet sein.

Der Basler Verleger Johann Herwegen witterte ein hervorragendes Geschäft und publizierte 1537 eine Gesamtausgabe der Werke des griechischen Mathematikers. Sie enthält weit mehr als die seit dem Mittelalter bekannten Elemente. Der Käufer erhielt zusätzlich die für Künstler so wichtige Optik und einige weitere kleinere Schriften des großen Mathematikers, die uns an dieser Stelle nicht zu interessieren brauchen. Auf jeden Fall freut sich das MoneyMuseum, dass es ihm auf der Stuttgarter Antiquariatsmesse 2020 gelungen ist, ein Exemplar beim Salzburger Antiquariat Johannes Müller zu erwerben.

Wieso schreibt ein Reformator ein Vorwort zu Euklid?

Die im MoneyMuseum aufbewahrte Ausgabe des Euklid von 1537 ist etwas ganz Besonderes, denn der bekannte protestantische Theologe und Weggefährte Martin Luthers schrieb ein Vorwort dazu. Das sollte uns nicht verwundern: Das Interesse von humanistischen Wissenschaftlern und Theologen an der Mathematik war enorm. Sie fühlten sich vor allem von der jüdischen Kabbalistik inspiriert. Ziel der Kabbala ist es, die Buchstaben der Bibel in Zahlenwerte umzusetzen, um durch komplizierte mathematische Berechnungen Einsicht in Gottes Plan zu erhalten. Das leuchtete – zumindest damals – auch protestantischen Theologen ein, die davon ausgingen, dass das Ende der Welt nahe sei.

Ein persönlicher Freund Martin Luthers, der Pfarrer Michael Stifel, war für seine Versuche bekannt, das Datum des Weltuntergangs mittels der Mathematik zu berechnen. Er fixierte es auf die 8. Stunde des 19. Oktober 1533. Und als die Welt dann doch nicht unterging, nahm er an der Universität von Wittenberg das Studium der Mathematik auf, um zu einem der bedeutendsten deutschen Mathematiker zu werden. Melanchthon verfasste zu seiner Arithmetica Integra genauso ein Vorwort wie er es für unsere Neuausgabe des Euklid tat. Schließlich war es ihm ein Herzensanliegen, mit seiner wissenschaftlichen Autorität die Belange der Mathematik zu fördern. Es dürfte zum Beispiel Melanchthon zu verdanken gewesen sein, dass die Universität Wittenberg überhaupt Lehrstühle für das Fach Mathematik besaß.

Eines hatte der Basler Verleger Johann Herwegen allerdings nicht in Betracht gezogen: Melanchthon war durch sein vehementes Eintreten für die Reformation in der wissenschaftlichen Welt umstritten. Und das bedeutete, dass kein katholischer Gläubiger, geschweige denn eine katholische Bibliothek ein Buch kaufen wollte, in dem das Vorwort eines Reformators abgedruckt war. Die nächsten Ausgaben des Euklid sollten ohne dieses Vorwort publiziert werden und sich weit besser verkaufen.

Als Albrecht Dürer im Jahr 1505 nach Venedig reiste, war er ein selbstbewusster Künstler, der hoffte, mit den venezianischen Kunsthändlern ins Geschäft zu kommen. Er hatte mit seinen handwerklich hervorragend gemachten Kupferstichen ein Produkt geschaffen, das günstig in der Herstellung war und in beliebigen Mengen reproduziert werden konnte. Ein Verkaufsschlager für den sich rasant entwickelnden Kunstmarkt. Seine Frau war äußerst erfolgreich darin, diese Kupferstiche auf dem deutschen Markt zu platzieren. Warum sollte ihm das nicht auch im Mekka des internationalen Kunsthandels Venedig gelingen?

Doch bei seiner Ankunft erlebte Dürer erst einmal einen Schock: Die Meister der Lagunenstadt waren ihm, der sich für einen Ausnahmekünstler gehalten hatte, weit voraus. Seine Konkurrenten beherrschten die Perspektive und schufen Gemälde von einer Realistik, die Albrecht Dürer beim besten Willen nicht nachzuahmen wusste. Auch an seiner Verwendung von Farben schnöselte die venezianische Konkurrenz herum. 

Als der junge Mann nun in den Werkstätten nachzufragen begann, wie diese überwältigenden Bilder zustande gekommen seien, gaben die Befragten keine Auskunft. Sie dachten gar nicht daran, einem Konkurrenten zu helfen, ihren Wissensvorsprung aufzuholen.

Was blieb Dürer also anderes übrig, als auch dem Buchmarkt sein Glück zu versuchen? Und wieder scheiterte er: Er fand kein einziges Buch zu diesem Thema – und Venedig war damals das europäische Zentrum der Buchproduktion!

Artikeltext:

Dürer kommt mit der Mathematik in Kontakt

Albrecht Dürer blieb also nichts anderes übrig, als sich einen Lehrer zu suchen, der ihm diese Technik – selbstverständlich gegen ein ordentliches Lehrgeld – vermittelte. Wir wissen, dass er zu diesem Zweck nach Bologna ritt. Nicht wissen wir dagegen, wer ihn als Schüler aufnahm. Allerdings gibt es einige Hinweise dafür, dass es der bekannte Mathematiker Pacioli gewesen sein könnte, den wir schon in unserem ersten Beitrag zum Thema Mathematik kennengelernt haben.

Der Franziskanermönch Luca Pacioli (1445-1514) zählte zu den bedeutendsten Mathematikern seiner Zeit. Er verfasste im Jahre 1494 das erste Lehrbuch zur doppelten Buchführung. Und er beschäftigte sich ausführlich mit der Perspektive beziehungsweise mit den – wie er sein wohl bekanntestes Werk nannte – „göttlichen Proportionen“. 1509 erschien in Venedig das gleichnamige Buch.

Pacioli war der festen Überzeugung, dass ein Mathematiker den vom Schöpfer nach göttlichen Gesetzen eingerichteten Kosmos verstehen könne. Die Mathematik sei die Sprache, in der Gott kommuniziere. Perfekte mathematische Gebilde spiegelten deshalb etwas vom göttlichen Geist.

Leonardo da Vinci, mit dem Pacioli in Mailand in stetem Austausch stand, sah das genauso. Er schuf sein heute noch weltweit berühmtes letztes Abendmahl mit Hilfe aufwändiger mathematischer Berechnungen zur Perspektive. Pacioli hat ihm mit an Sicherheit grenzender Wahrscheinlichkeit dabei geholfen. So gelang es dem Ausnahmekünstler, jeden, der an einem bestimmten Punkt des Speisesaals im Dominikanerkloster Santa Maria delle Grazie stand, in das wunderbare Geschehen einzubeziehen. Die Mathematik verband die menschliche mit der göttlichen Welt und machte göttliches Geschehen für den Menschen greifbar.

Man kann sich gut vorstellen, welche tiefschürfenden Gespräche der Mathematiker und der Künstler geführt haben müssen. Eines ihrer Resultate war etwas, das heute als „Goldener Schnitt“ bekannt ist. Welches Verhältnis müssen zwei Seiten zueinander haben, um ein wohlproportioniertes Rechteck zu formen? Pacioli fixierte dieses „göttliche“ Zahlenverhältnis in seinem Werk auf annähernd 1:1,6180339. Der Franziskanermönch liebte die symmetrischen Gebilde und fand in ihnen einen Abglanz des Göttlichen. Wie eng Leonardo da Vinci in die Entstehung von Paciolis 1509 publiziertem Buch „De divina proportione“ involviert war, zeigt die Tatsache, dass er 60 Zeichnungen dazu beisteuerte.

Wenn Albrecht Dürer tatsächlich von diesem begnadeten Mathematiker in die Kunsttheorie eingeführt wurde, versteht man, warum er bis ins hohe Alter versuchte – in Nachahmung zum Goldenen Schnitt –, die Zahlen zu finden, auf deren Grundlage es Künstlern möglich sein würde, den perfekten Menschen zu schaffen.

Aber wie gesagt, es ist nur eine wohl begründete Vermutung, dass Dürer bei Pacioli lernte. Sicher dagegen wissen wir, dass er – wahrscheinlich auf Rat seines Lehrers hin – für einen Gulden den im Jahr 1507 in Venedig erschienenen Druck der für seine Zwecke wichtigsten Werke Euklids erwarb: Dessen „Optik“ lieferte ihm die theoretische Begründung der Perspektive; und dessen „Elemente“ gaben ihm die Mittel in die Hand, mit Zirkel und Lineal den für die Perspektive notwendigen Fluchtpunkt zu konstruieren.

Ein Buch über die Beherrschung der Malerei

Dürer wird sich mit den in Italien gelernten neuen Methoden eine völlig neue Welt eröffnet haben. Und er wollte – anders als seine italienischen Konkurrenten – seine Kollegen an dem Wissen teilhaben lassen. Vielleicht beflügelte ihn auch die Überzeugung, dass einzig er als der herausragende Künstler seiner Zeit in der Lage sei, ein epochales Buch über die Malerei zu verfassen, und dass dieses Buch seinen Ruhm in alle Welt und bis in fernste Jahrhunderte transportieren werde.

Er sollte allerdings am Umfang seines Vorhabens scheitern. Die Aspekte der Malerei – von der technischen Vorbereitung der Leinwand, über die Komposition des Gemäldes und die Bereitung der Farben, bis hin zum richtigen Farbauftrag – waren einfach zu vielfältig, um neben der täglichen Arbeit ein wirkliches Grundlagenwerk zu verfassen. Dürers Einführung in die Malkunst kam über Vorwort, Inhaltsangabe und grobe Entwürfe einzelner Teilkapital nie hinaus. Irgendwann wird er die Unausführbarkeit seines Plans eingesehen haben, weil er sich auf ein kleines Teilkapitelchen konzentrierte: 1525 erschien Dürers „Unterweisung zur Messung mit dem Zirkel und dem Lineal“.

Von der Geometrie zum Göttlichen

Darin schreibt Albrecht Dürer in deutscher Sprache all die Inhalte nieder, die er sich selbst mit Hilfe seines italienischen Lehrers und des lateinischen Eukliddrucks mühsam erarbeiten musste. Er erklärt seinem Leser, wie man geometrische Objekte mit Hilfe von Zirkel und Lineal konstruiert, dass sich aber nicht alle geometrischen Formen konstruieren lassen, dass man vielmehr gelegentlich auf die Handzeichnung angewiesen sei. Dabei hat er ständig die Praxis im Blick. Sein Buch ist für Maler und Baumeister gemacht, aber auch für Schreiner, deren Kunden immer häufiger ein mathematisch aufwändig zu berechnendes Parkett bestellten. Dürer gibt den deutschen Handwerkern das Werkzeug an die Hand, mit der italienischen Konkurrenz mithalten zu können. So erklärt er zum Beispiel die Funktionsweise eines Perspektografen für alle, die nicht wie er in der Lage sind, komplexe Figuren freihändig zu malen. Mit einem Perspektografen konnte ein Maler ein Motiv maschinell erfassen. Perspektivische Genauigkeit wurde so zur Fleißarbeit, ein Verfahren, das der berühmte Schöpfer venezianischer Veduten, Canaletto zur Vollkommenheit perfektionieren sollte.

Bereits zwei Jahre nach seinem Erstlingswerk publizierte Albrecht Dürer ein weiteres Buch, in dem er die geometrischen Grundlagen für den Festungsbau zusammenstellte. Alle großen Künstler der Renaissance waren gleichzeitig Ingenieure und entwarfen für ihre Mäzene nicht nur Festdekorationen, sondern auch Befestigungsbauten.

Eines aber beschäftigte Albrecht Dürer unentwegt, selbst während er diese eher pragmatischen Bücher verfasste: Die Frage, wie die menschlichen Proportionen berechnet werden könnten, um den „schönen“, den „perfekten“ Menschen zu entwerfen, den Menschen, in dem sich die göttliche Schöpfung spiegelt. Diesem Thema widmete Albrecht Dürer sein wohl bekanntestes Werk. Es erschien 1528 unter dem Titel „Vier Bücher von menschlicher Proportion“. Das MoneyMuseum besitzt ein etwas späteres Exemplar in italienischer Sprache. Es wurde im Jahre 1591 in Venedig publiziert.

Was aber die Schönheit ist, das weiß ich nicht!

Albrecht Dürer, der Mann, der gelernt hatte, die Natur um sich herum perfekt abzubilden, kreiste in diesem Buch um die grundsätzliche Frage, wann ein menschlicher Körper als „schön“ wahrgenommen wird. Während wir heute eher Psychologen zu diesem Thema befragen würden, ging Albrecht Dürer einen anderen Weg. Für ihn war es selbstverständlich, dass das Schöne und das Göttliche nahe beeineinander liegen mussten. Deshalb konnte sich die Schönheit nur in einem verstecken: In dem Menschen als Krone der Schöpfung. 

Dürer nahm also einen Maßstab in die Hand und begann Menschen zu vermessen, um so durch eine gewaltige Menge an Daten dem Schöpfer auf die Schliche zu kommen. Er sammelte ein gigantisches Zahlenwerk, von dem uns nur ein Bruchteil in seinem Buch überliefert ist. Er übersäte den menschlichen Körper mit mehr als 100 Meßpunkten und sammelte Jahr für Jahr neues Datenmaterial – er selbst schreibt, er habe zwei- bis dreihundert Personen ausgemessen – , um mathematisch zu formulieren, wie Gott den Menschen geplant habe.

Seine Kollegen waren irritiert. Nur die wenigsten verstanden, was Dürer mit seinem Buch wollte. Selbst sein genialer Künstlerkollege Michelangelo äußerte amüsiert. Er spottete, dass Dürers Figuren „steif wie Pfähle“ seien. Natürlich waren sie das. Es ging Dürer ja nicht darum, lebende Menschen zu zeichnen, sondern Musterfiguren, anhand derer er Typen herauskristallisierte. Über diese legte er ein engmaschiges Gitter, das ihm half zu berechnen, wie sich die Perspektive veränderte, sobald sich ein Körperteil bewegte.

Dürer war seiner Zeit damit weit voraus. Heute versteht jeder, der sich mit Computeranimation von Trickfilmfiguren beschäftigt, sofort, welchen Nutzen Dürers Berechnungen hatten. Sie halfen, die exakte perspektivische Wiedergabe von Körperbewegungen zu berechnen, ohne mühsam mit Skizzen herumprobieren zu müssen. Berechnungen wie diese sind heute die technische Grundlage in jedem Trickstudio.

So genial und innovativ Dürers Überlegungen auch waren, eines schaffte er mit seiner Datenorgie nicht: Den idealen Menschen zu finden. Resigniert gab der alt gewordene Großmeister der deutschen Malerei zu, dass der Schöpfer die Menschen eben so gemacht habe, wie sie sein müssten. Die wahre Wohlgestalt und Schönheit wohne ihnen allen inne.

Damit hatte er Recht. Das mussten auch seine modernen Nachfahren im Trickfilm-Business lernen. Sie schufen einige sehr teure Flops, bis sie begriffen, dass die Computeranimation ihre Grenzen hat. Das Publikum will im Zeichentrickfilm keine exakt imitierte Realität sehen. Im Gegenteil. Das menschliche Auge erfreut sich an den Abweichungen vom Normalen, die eine Zeichnung charmant und einen Menschen einmalig machen. 

Man bekommt sie in den meisten Antiquariaten für sehr wenig Geld, jene langweiligen Rechentabellen, in denen Seite für Seite die Resultate von Multiplikationen aufgelistet sind. Man nennt sie Barreme, nach dem französischen Mathematiker François-Bertrand Barrême (1638-1703), einem Professor für Mathematik, dessen Verdienste um das Buchhaltungswesen uns an dieser Stelle nicht weiter beschäftigen sollen. Wir wollen uns vielmehr fragen, warum man noch zu Beginn des 19. Jahrhunderts Bücher mit sich herumschleppte, um das Resultat einer Multiplikation zu erfahren, statt einfach ein Stück Papier zu nehmen und selbst zu rechnen.

Artikeltext:

Das Rechnen auf der Linie

Um das zu verstehen, müssen wir ein paar Selbstverständlichkeiten unseres Lebens in Frage stellen. Zu diesen gehört das kleine 1x1, die arabischen Zahlen und das Wissen, dass sich in Zehnerschritten am einfachsten rechnen lässt. Es gab nämlich nichts davon, als sich im 8. Jahrhundert eine theoretische Währung durchsetzte. Sie beruhte auf dem Pfund, einem Pfund, das in 20 Schillinge resp. 240 Pence unterteilt war. Das karolingische System – man schrieb lange Jahre Karl dem Großen seine Einführung zu – war im Alltag sehr praktisch, da die Zahl 12, auf der es beruht, wesentlich besser zu teilen ist, als die 10. 12 kann man durch 1, 2, 3, 4 und 6 teilen, während die 10 nur durch 1, 2 und 5 teilbar ist.

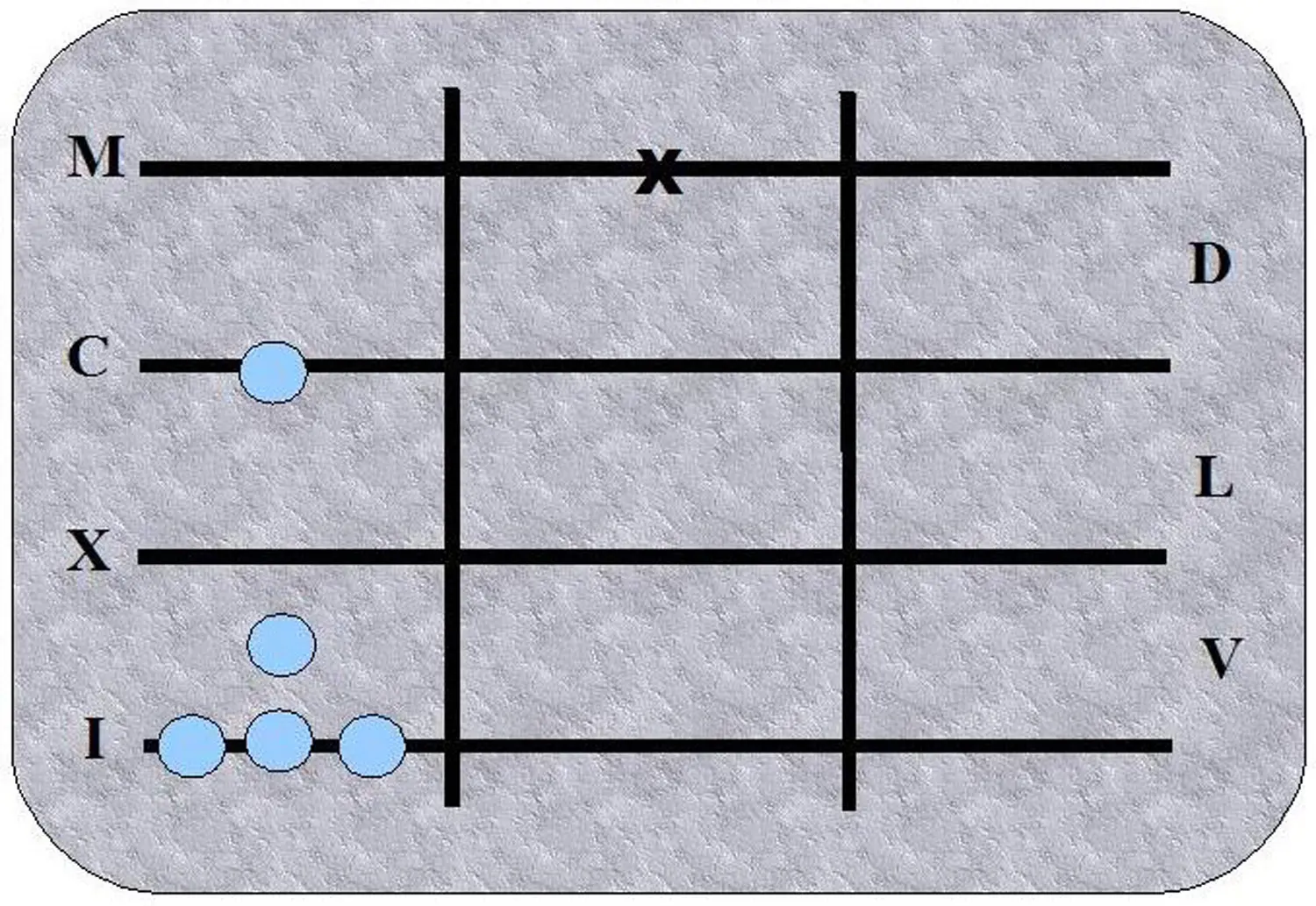
Für das Rechnen machte es keinen wesentlichen Unterschied, denn schriftliches Rechnen funktionierte nicht mit den lateinischen Zahlen, die in Zentraleuropa die Kaufmannsbücher bis ins 15. Jahrhundert beherrschten. Stattdessen benutzte man den Abakus oder Rechentisch, um Additionen und Subtraktionen „auf der Linie“ auszuführen.

Der Umgang mit so einem Rechentisch ist derart einfach, dass moderne Menschen Schwierigkeiten haben, ihn sich überhaupt vorzustellen. Statt abstrakt zu denken, muss man nur Steine hinlegen und zählen – eigentlich genauso wie ein Kleinkind heute mit den Fingern rechnet – nur etwas professioneller und mit größeren Zahlen. Mit anderen Worten. Wenn ich 3 zu 4 addieren will, lege ich erst drei, dann vier Steine hin und zähle danach, wie viele Steine es sind. Will ich 4+3+2+3 rechnen, lege ich erst vier Steine hin, dann drei, dann zwei, dann drei – und zähle nach, ja, das hatten wir schon.

Damit das Zählen etwas übersichtlicher wird, gibt es mehrere Linien. War auf der untersten Linie die 5 erreicht, wurden die fünf Steine weggenommen und dafür ein Stein in die Mitte verschoben. Lagen zwei Steine in der Mitte, nahm man sie weg und ersetzte sie durch einen weiteren Stein auf der nächsten Linie.

Und das war’s. Jeder konnte so rechnen, allerdings nur in begrenztem Ausmaß. Beim Subtrahieren nahm man einfach die Steine für die Zahl weg, die man abziehen wollte. Natürlich nur solange noch Steine da waren. Negative Zahlen kannte das Zahlenbrett nicht. Multiplizieren funktionierte super, denn 3x3 ist letztendlich nichts anderes als 3+3+3. Wenn die Rechnung allerdings 167x56 lautete, dann war schon einiges an Arbeit notwendig, um sie auszuführen. Dividieren? Vergessen Sie’s. Das war höhere Mathematik und bereitete den Kaufleuten echt Probleme.

Die Zahlen, die man zusammen mit dem Rechentisch benutzte, waren die lateinischen Zahlen. Sie waren optimal an das System angepasst. Schauen wir uns das an einem Beispiel an. Das kommende Jahr 2022 würde in lateinischer Schrift so aussehen: MMXXII. Ich bin mir sicher, Sie verstehen sofort, auf welche Linien Sie Ihre Steine legen müssen, um diese Zahl auszudrücken. Einfach zwei auf die M-Linie (Tausender), zwei auf die X-Linie (Zehner) und zwei auf die I-Linie (Einer).

Mit den mittelalterlichen Nominalen rechnen

Wer mit Münzen rechnete, musste nur die Stücklungen ändern, für die die einzelnen Linien standen. Dann repräsentierte die unterste Linie die Pfennige, die mittlere Linie die Schillinge und die oberste Linie die Pfunde. Bereinigt wurde einfach in einem anderen Rhythmus, also wenn sich 6 Steine auf der Pfennig-Linie angesammelt hatten, oder 10 Steine auf der Schilling-Linie. Für einen Händler machte es vom Verfahren her keinen Unterschied, ob er Äpfel addierte oder Geld.

Und dann kamen die arabischen Zahlen

Allerdings stießen die Händler in ihrem Alltag oft auf praktische Probleme, wenn sie so rechneten. Stellen Sie sich vor, dass drei Händler ihr Kapital zusammenlegen, um eine Karawane auszustatten. Der eine gibt 20, der zweite 35, der dritte 49 Gulden. Und jetzt rechnen Sie auf dem Rechenbrett aus, wie viel von den 218 Gulden Gewinn jedem einzelnen von ihnen anteilig zusteht. Ein Alptraum!

Sie können sich vorstellen, wie begeistert die italienischen Fernkaufleute waren, als sie das erste Mal in der arabischen Welt auf die arabischen Zahlen und das schriftliche Rechnen stießen. Die modernen Zahlen plus die Null als Platzhalter ermöglichten nicht nur eine völlig neue Form der Addition, sondern auch die Multiplikation – wenn man in der Schule das kleine 1x1 gelernt hatte. Das gehört seit damals zum Lehrplan. Auf einmal klappte auch die Division, es gab negative Ergebnisse, Brüche, und last but not least die Rechnung mit einer Unbekannten. Übrigens, all unsere so selbstverständlichen mathematischen Zeichen wie +, -, = usw. entstanden erst in der Renaissance, in der die Rechnerei mit den arabischen Zahlen einen echten Boom erlebte und sich das neue System über ganz Europa verbreitete.

Der träge Mensch

Das Problem an der ganzen Angelegenheit ist, dass die neuen Zahlen das Dezimalsystem bevorzugen. Wenn Sie mir nicht glauben, versuchen Sie’s einfach selbst einmal und rechnen schriftlich 48 cm + 16 cm + 23 cm + 47 cm in Meter um. Und jetzt machen Sie dasselbe mit Minuten. Also wie viel Stunden sind 48 min + 16 min + 23 min + 47 min?

Nun ist aber der Mensch so beschaffen, dass er keinerlei Lust hat, sich an neue Maße und Einheiten zu gewöhnen, nur weil die alten nicht mehr zu seinem Rechensystem passen. In Westeuropa zum Beispiel wurde erst rund drei Jahrhunderte, nachdem sich die neue Art zu rechnen durchgesetzt hatte, eine auf dem Dezimalsystem basierende Währung eingeführt: Die französische Revolution zwang ihren vernunftbegabten Bürger ein vernünftiges Geldsystem auf. Wie gerne der Mensch unvernünftig ist, sieht man daran, wie schnell viele der von Frankreich annektierten Staaten, die sich an den Freuden des Fortschritts hatten delektieren dürfen, wieder zu ihrem herrlich unvernünftigen alten Geldsystem zurückkehrten. Die nie von Frankreich eroberten Briten blieben bis 1971 dabei.

Und deshalb brauchte es den Baremme

Und damit sind wir bei unserem Büchlein gelandet, denn die Livres, Deniers und Sous ließen sich eben nicht auf dem Papier multiplizieren. Rechentische benutzte man auch nicht mehr. Stattdessen holte ein Kaufmann dieses Büchlein aus der Tasche, wenn er sich fragte, was er zahlen müsse, wenn er nicht exakt ein Pfund Pfeffer kaufte, sondern ein drei Viertel Pfund, fünf Pfund oder gar 973 ½ Pfund.

Wir haben also mit diesem kleinen, unscheinbaren Büchlein, das wir für 30 Euro im Heidelberger Antiquariat Hatry gekauft haben, ein Zeugnis für den Übergang von den römischen zu den arabischen Zahlen in der Hand und für den Schwierigkeit der Menschheit, sich adäquat an Neuerungen anzupassen.

Stellen wir uns die bäuerliche Welt des 18. Jahrhunderts vor. Das Leben im kleinen Dorf ist geprägt von den täglichen Verrichtungen. Pflügen, säen, ernten, die Winterruhe, dazwischen die kirchlichen Feste - je nach Gegend katholisch oder protestantisch. Und das ist es dann. Nur ein relativ kleiner Teil der dörflichen Bevölkerung kann lesen. Eine Zeitung leistet sich niemand, und Besuch aus der großen weiten Welt gibt es kaum.

In dieser Gesellschaft hatten die von der modernen Forschung so genannten „Volkskalender“ großen Erfolg. Sie waren zwar auch ein Kalender, hatten aber noch viele weitere Funktionen.

Artikeltext:

Heiliger, Mondphase, Aderlass

Stellen wir uns eine Welt ohne die Tagesschau vor, ohne den täglichen Wetterbericht, und das obwohl die Menschen damals in weit höherem Maß vom Wetter abhängig waren, als wir das heute sind. In dieser Welt war der Kalender von entscheidender Bedeutung. Man konsultierte ihn regelmäßig. Deshalb hing er in der Schweiz gerne in einem eigens für ihn angefertigten Rahmen an der Wand der guten Stube. Wie häufig diese Kalender zur Hand genommen wurden, sieht man daran, wie zerlesen sie sind.

So ein Kalender teilte dem Bauern nicht nur mit, welches Datum man heute schrieb, und ob es sich um einen Kirch- oder Arbeitstag handelte. Er erfuhr auch, für welche Tätigkeiten sich der Tag besonders gut eignete. War es gut, an diesem Tag den Acker zu bestellen, das Holz zu fällen, die Haare abzuschneiden? War der Tag mehr oder weniger gut geeignet, um zur Ader zu lassen? Wenn mancher Gärtner heute darauf besteht, dass er mit dem Mondkalender ganz besonders gute Gartenergebnisse erzielt, dann greift er auf ein Mittel zurück, das der bäuerliche Bevölkerung des 18. Jahrhunderts als Hilfsmittel diente, weil sie eben keine anderen hatte.

Für alle, die sich kein teures personalisiertes Horoskop leisten konnten, gab es im Volkskalender das Sternzeichen mit dem Aszendenten des Tages zum Sondertarif. Dazu ersetzten die Bauernregeln den Wetterbericht und eine Liste informierte über die wichtigsten Märkte des Monats. 

Ein Blick in die Welt - aber bitte in einfacher Sprache

Das war die Basisversion, die der Hausierer für 2 1/2 Kreuzer an der Tür verkaufte. Für 5 Kreuzer gab es den großen Kalender, in dem sich alles fand, was wir heute in einer Boulevardzeitschrift erwarten würden - nur halt nicht einmal pro Tag, sondern einmal pro Jahr. 5 Kreuzer waren nicht viel in einer Welt, in der selbst eine Wäscherin 12 1/2 Kreuzer, ein Schneider 30 Kreuzer am Tag verdiente. Deshalb waren Publikationen wie der Appenzeller Kalender so weit verbreitet.

Die Nachrichten stammten - wie noch heute in jeder guten Zeitung - aus der näheren Umgebung und dem Rest der Welt. Schauen wir uns doch an, was die beiden im MoneyMuseum liegenden Kalender zu bieten haben. Da gibt es für die nähere Umgebung einen Nachruf auf den verstorbenen Abt von St. Gallen, dazu die Namen all derer, die im Alter von über 90 Jahren verstorben sind, sowie eine Statistik der Geburten, der Sterbefälle und der Heiraten.

Die Nachrichten aus aller Welt werden der politischen Geographie nach geordnet. Dabei gilt die alte Regel: Umso näher, umso ausführlicher ist der Bericht. 

Wir freuen uns natürlich, wenn wir in diesen Kalendern auf Ereignisse stoßen, die wir aus unserem Geschichtsunterricht kennen: So zeigt der Appenzeller Kalender von 1797 ein Porträt des jungen Napoleon Bonaparte, der gerade Italien aufmischte. Der Kalender von 1793 vermerkt die spektakuläre Ermordung des schwedischen Königs Gustavs III., räumt ihr aber wesentlich weniger Raum ein, als dem Tod von Kaiser Leopold II. Die benachbarten Habsburger waren den Appenzellern eben näher als die Schweden im hohen Norden.

Alle Texte sind in einfacher Sprache gehalten. Sie wollen belehren, aber ohne Überheblichkeit. Sie greifen Themen auf, von denen auch ein Bauer etwas gehört haben konnte, so zum Beispiel die Ostindische Handelskompanie, die ganz Europa mit den neuen Kolonialwaren versorgte, die auch ein Bauer für viel Geld auf den Jahrmärkten vielleicht nicht kaufen, aber doch wenigstens sehen konnte.

Auf der Seite einer bäuerlichen Bevölkerung

Volkskalender wie der Appenzeller Kalender kennen ihr Klientel und bedienen seine Bedürfnisse. Wer kam denn da noch mit, wenn der reiche Nachbar, bei dem man einen Kredit für eine Woche haben wollte, die Zinsen berechnete? Der Appenzeller Kalender machte es dem Zinsnehmer leicht zu überprüfen, ob der ihm vorgeschlagene Vertrag sich an den von der katholischen Kirche festgesetzten und als angemessen betrachteten Zinssatz in Höhe von 5 % hielt. Auch die Tabelle zum Multiplizieren war äußerst nützlich. Mit ihr konnte man diese schwierige Rechenform beherrschen - und das ohne Taschenrechner und höhere Schulbildung.  Dazu kam noch ein bisschen Allgemeinbildung. Kein Wunder, dass die Volkskalender in den gerade aufkommenden Volksschulen als Lesebücher genutzt wurden.

Dazu die Unterhaltung

Neben Bildung und Nützlichem boten die Volkskalender Unterhaltsames fürs ganze Jahr. Da gab es die Kalendergeschichten, die ein Johann Peter Hebel zu einer Kunstform machte. Noch beliebter war all das Skurrile, Spektakuläre und Merkwürdige, das heute noch die Menschheit dazu bringt, die Lektüre der Tageszeitung mit der Seite „Vermischtes“ zu beginnen.

Ein gutes Geschäft

Der Appenzeller Kalender war in der deutschsprachigen Schweiz wohl der am weitesten verbreitete Volkskalender, und so kann man ihn heute noch für sehr wenig Geld in vielen Antiquariaten und gut sortierten Brockenstuben erwerben - wie wir es getan haben. Das liegt daran, dass bis zu 60.000 Stück pro Jahr gedruckt wurden. Gegründet von Johannes Tobler im Jahr 1722, hatte in der zweiten Hälfte des 18. Jahrhunderts Ulrich Sturzenegger das Geschäft übernommen. Der kam aus dem Bauernstand, verfügte über keinerlei höhere Bildung und hatte sich all das mathematische und astronomische Wissen, das es brauchte, um so einen Kalender zusammenzustellen, selbst beigebracht. Für die beiden Kalender, die uns vorliegen, zeichnete sein Sohn Mathias Sturzenegger zusammen mit seinem Bruder verantwortlich, der sie in der hauseigenen Druckerei in Trogen produzierte.

Zu diesem Zeitpunkt war der Appenzeller Kalender übrigens nicht mehr konkurrenzlos. Der eifrige St. Galler Aufklärer Johannes Zollikofer hatte 1790 das „Christliche Jahrbuch ohne Aberglauben“ ins Leben gerufen. Sein Kalender verzichtete auf alle Horoskope und sparte dafür nicht mit Belehrungen. Er hatte gegen den Appenzeller Kalender keine Chance - und das nicht nur, weil er nicht 5, sondern 6 Kreuzer kostete.