Man bekommt sie in den meisten Antiquariaten für sehr wenig Geld, jene langweiligen Rechentabellen, in denen Seite für Seite die Resultate von Multiplikationen aufgelistet sind. Man nennt sie Barreme, nach dem französischen Mathematiker François-Bertrand Barrême (1638-1703), einem Professor für Mathematik, dessen Verdienste um das Buchhaltungswesen uns an dieser Stelle nicht weiter beschäftigen sollen. Wir wollen uns vielmehr fragen, warum man noch zu Beginn des 19. Jahrhunderts Bücher mit sich herumschleppte, um das Resultat einer Multiplikation zu erfahren, statt einfach ein Stück Papier zu nehmen und selbst zu rechnen.
Artikeltext:
Das Rechnen auf der Linie
Um das zu verstehen, müssen wir ein paar Selbstverständlichkeiten unseres Lebens in Frage stellen. Zu diesen gehört das kleine 1x1, die arabischen Zahlen und das Wissen, dass sich in Zehnerschritten am einfachsten rechnen lässt. Es gab nämlich nichts davon, als sich im 8. Jahrhundert eine theoretische Währung durchsetzte. Sie beruhte auf dem Pfund, einem Pfund, das in 20 Schillinge resp. 240 Pence unterteilt war. Das karolingische System – man schrieb lange Jahre Karl dem Großen seine Einführung zu – war im Alltag sehr praktisch, da die Zahl 12, auf der es beruht, wesentlich besser zu teilen ist, als die 10. 12 kann man durch 1, 2, 3, 4 und 6 teilen, während die 10 nur durch 1, 2 und 5 teilbar ist.
Für das Rechnen machte es keinen wesentlichen Unterschied, denn schriftliches Rechnen funktionierte nicht mit den lateinischen Zahlen, die in Zentraleuropa die Kaufmannsbücher bis ins 15. Jahrhundert beherrschten. Stattdessen benutzte man den Abakus oder Rechentisch, um Additionen und Subtraktionen „auf der Linie“ auszuführen.
Der Umgang mit so einem Rechentisch ist derart einfach, dass moderne Menschen Schwierigkeiten haben, ihn sich überhaupt vorzustellen. Statt abstrakt zu denken, muss man nur Steine hinlegen und zählen – eigentlich genauso wie ein Kleinkind heute mit den Fingern rechnet – nur etwas professioneller und mit größeren Zahlen. Mit anderen Worten. Wenn ich 3 zu 4 addieren will, lege ich erst drei, dann vier Steine hin und zähle danach, wie viele Steine es sind. Will ich 4+3+2+3 rechnen, lege ich erst vier Steine hin, dann drei, dann zwei, dann drei – und zähle nach, ja, das hatten wir schon.
Damit das Zählen etwas übersichtlicher wird, gibt es mehrere Linien. War auf der untersten Linie die 5 erreicht, wurden die fünf Steine weggenommen und dafür ein Stein in die Mitte verschoben. Lagen zwei Steine in der Mitte, nahm man sie weg und ersetzte sie durch einen weiteren Stein auf der nächsten Linie.
Und das war’s. Jeder konnte so rechnen, allerdings nur in begrenztem Ausmaß. Beim Subtrahieren nahm man einfach die Steine für die Zahl weg, die man abziehen wollte. Natürlich nur solange noch Steine da waren. Negative Zahlen kannte das Zahlenbrett nicht. Multiplizieren funktionierte super, denn 3x3 ist letztendlich nichts anderes als 3+3+3. Wenn die Rechnung allerdings 167x56 lautete, dann war schon einiges an Arbeit notwendig, um sie auszuführen. Dividieren? Vergessen Sie’s. Das war höhere Mathematik und bereitete den Kaufleuten echt Probleme.

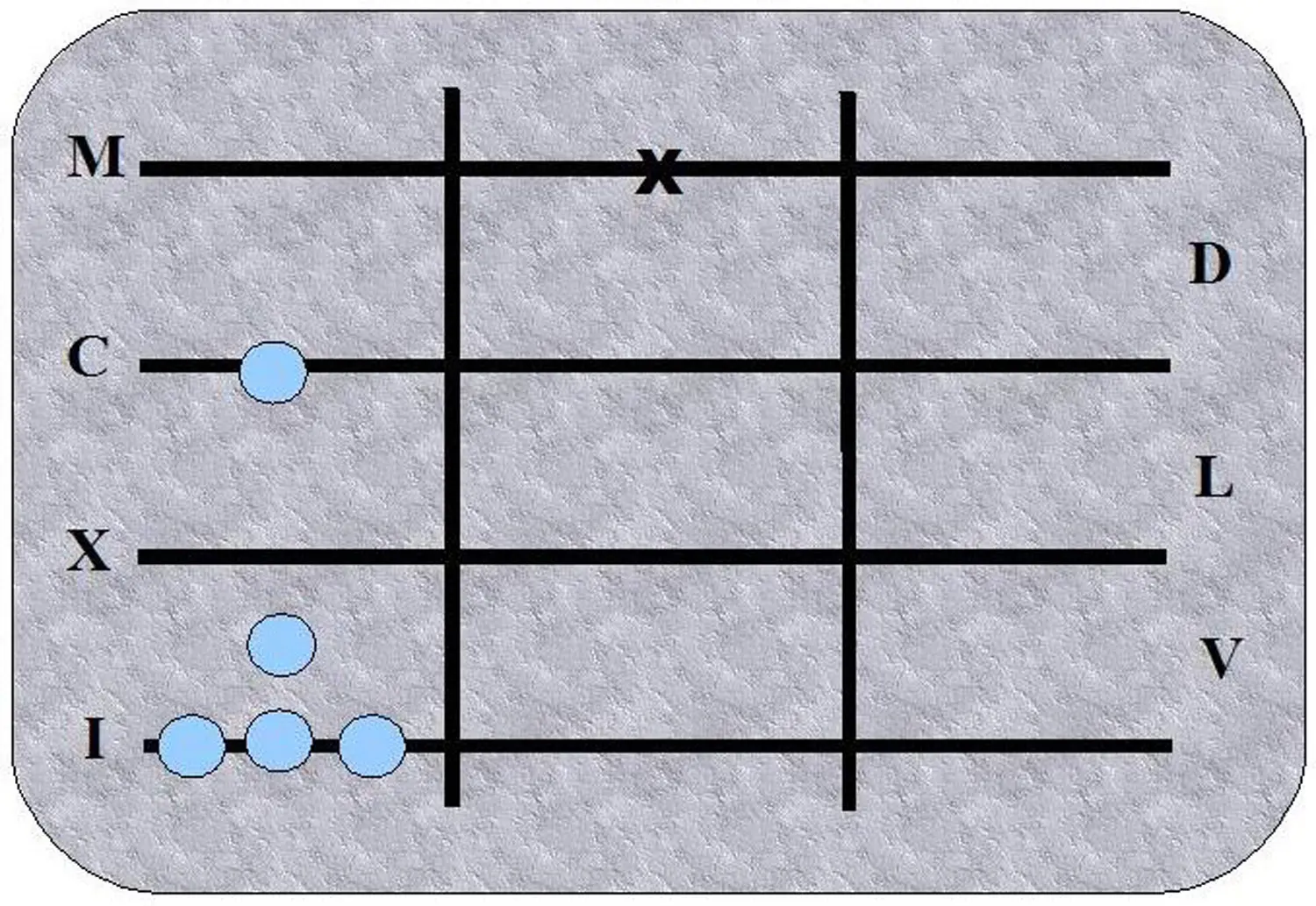
Die Zahlen, die man zusammen mit dem Rechentisch benutzte, waren die lateinischen Zahlen. Sie waren optimal an das System angepasst. Schauen wir uns das an einem Beispiel an. Das kommende Jahr 2022 würde in lateinischer Schrift so aussehen: MMXXII. Ich bin mir sicher, Sie verstehen sofort, auf welche Linien Sie Ihre Steine legen müssen, um diese Zahl auszudrücken. Einfach zwei auf die M-Linie (Tausender), zwei auf die X-Linie (Zehner) und zwei auf die I-Linie (Einer).
Mit den mittelalterlichen Nominalen rechnen
Wer mit Münzen rechnete, musste nur die Stücklungen ändern, für die die einzelnen Linien standen. Dann repräsentierte die unterste Linie die Pfennige, die mittlere Linie die Schillinge und die oberste Linie die Pfunde. Bereinigt wurde einfach in einem anderen Rhythmus, also wenn sich 6 Steine auf der Pfennig-Linie angesammelt hatten, oder 10 Steine auf der Schilling-Linie. Für einen Händler machte es vom Verfahren her keinen Unterschied, ob er Äpfel addierte oder Geld.

Und dann kamen die arabischen Zahlen
Allerdings stießen die Händler in ihrem Alltag oft auf praktische Probleme, wenn sie so rechneten. Stellen Sie sich vor, dass drei Händler ihr Kapital zusammenlegen, um eine Karawane auszustatten. Der eine gibt 20, der zweite 35, der dritte 49 Gulden. Und jetzt rechnen Sie auf dem Rechenbrett aus, wie viel von den 218 Gulden Gewinn jedem einzelnen von ihnen anteilig zusteht. Ein Alptraum!
Sie können sich vorstellen, wie begeistert die italienischen Fernkaufleute waren, als sie das erste Mal in der arabischen Welt auf die arabischen Zahlen und das schriftliche Rechnen stießen. Die modernen Zahlen plus die Null als Platzhalter ermöglichten nicht nur eine völlig neue Form der Addition, sondern auch die Multiplikation – wenn man in der Schule das kleine 1x1 gelernt hatte. Das gehört seit damals zum Lehrplan. Auf einmal klappte auch die Division, es gab negative Ergebnisse, Brüche, und last but not least die Rechnung mit einer Unbekannten. Übrigens, all unsere so selbstverständlichen mathematischen Zeichen wie +, -, = usw. entstanden erst in der Renaissance, in der die Rechnerei mit den arabischen Zahlen einen echten Boom erlebte und sich das neue System über ganz Europa verbreitete.
Der träge Mensch
Das Problem an der ganzen Angelegenheit ist, dass die neuen Zahlen das Dezimalsystem bevorzugen. Wenn Sie mir nicht glauben, versuchen Sie’s einfach selbst einmal und rechnen schriftlich 48 cm + 16 cm + 23 cm + 47 cm in Meter um. Und jetzt machen Sie dasselbe mit Minuten. Also wie viel Stunden sind 48 min + 16 min + 23 min + 47 min?
Nun ist aber der Mensch so beschaffen, dass er keinerlei Lust hat, sich an neue Maße und Einheiten zu gewöhnen, nur weil die alten nicht mehr zu seinem Rechensystem passen. In Westeuropa zum Beispiel wurde erst rund drei Jahrhunderte, nachdem sich die neue Art zu rechnen durchgesetzt hatte, eine auf dem Dezimalsystem basierende Währung eingeführt: Die französische Revolution zwang ihren vernunftbegabten Bürger ein vernünftiges Geldsystem auf. Wie gerne der Mensch unvernünftig ist, sieht man daran, wie schnell viele der von Frankreich annektierten Staaten, die sich an den Freuden des Fortschritts hatten delektieren dürfen, wieder zu ihrem herrlich unvernünftigen alten Geldsystem zurückkehrten. Die nie von Frankreich eroberten Briten blieben bis 1971 dabei.
Und deshalb brauchte es den Baremme
Und damit sind wir bei unserem Büchlein gelandet, denn die Livres, Deniers und Sous ließen sich eben nicht auf dem Papier multiplizieren. Rechentische benutzte man auch nicht mehr. Stattdessen holte ein Kaufmann dieses Büchlein aus der Tasche, wenn er sich fragte, was er zahlen müsse, wenn er nicht exakt ein Pfund Pfeffer kaufte, sondern ein drei Viertel Pfund, fünf Pfund oder gar 973 ½ Pfund.
Wir haben also mit diesem kleinen, unscheinbaren Büchlein, das wir für 30 Euro im Heidelberger Antiquariat Hatry gekauft haben, ein Zeugnis für den Übergang von den römischen zu den arabischen Zahlen in der Hand und für den Schwierigkeit der Menschheit, sich adäquat an Neuerungen anzupassen.






