The Long Way to the Decimal System

In most antiquarian bookshops, you can get them for very little money, those boring arithmetic tables in which the results of multiplications are listed on pages on end. They are called “barremes”, after the French mathematician François-Bertrand Barrême (1638-1703), a professor of mathematics whose contributions to accounting will not be dealt with in this article. Instead, we will ask ourselves why people were still carrying books around at the beginning of the 19th century to find out the result of multiplications instead of simply taking a piece of paper and doing the calculation themselves.

Artikeltext:

Calculating on the Line

To understand this, we have to question a few things we take for granted in our lives. These include having memorized the multiplication table from 1 to 10, Arabic numbers and the knowledge that the easiest way to calculate is in steps of ten. None of these things existed when a theoretical currency established itself in the 8th century. It was based on the pound – and one pound could be divided into 20 shillings or 240 pence. The Carolingian system – for many years Charlemagne was believed to have introduced it – was very practical in everyday life because the number 12 it was based on is much easier to divide than 10. 12 can be divided by 1, 2, 3, 4, and 6 whereas 10 can only be divided by 1, 2 and 5.

For arithmetic it made no significant difference, because written arithmetic did not work with the Latin numbers that dominated merchant books in Central Europe until the 15th century. Instead, the abacus or counting table was used to perform addition and subtraction “on the line”.

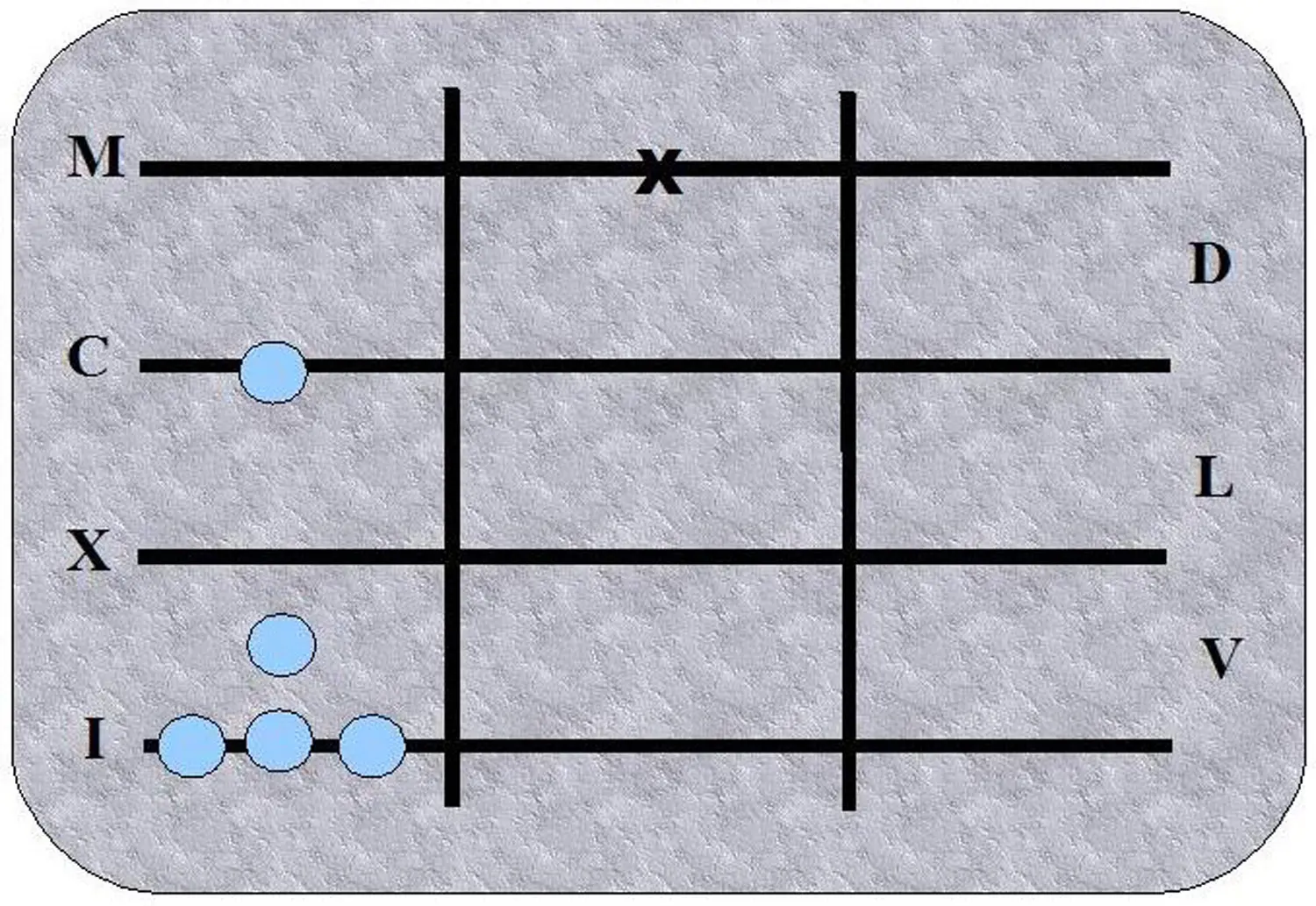
Using such a counting table is so easy that even imagining it is difficult for modern people. Instead of thinking abstractly, all you have to do is put down stones and count them – in fact, just as small children count their fingers to calculate – only a little more professional and with larger numbers. In other words: If I want to add 3 to 4, I first put down three, then four stones; then I count how many stones there are. If I want to calculate 4+3+2+3, I first put down four stones, then three, then two, then three – and count them, yes, we’ve got that now.

To make counting a bit easier, there are several lines. If the number 5 was reached on the lowest line, the five stones were taken away and one stone was placed in the middle. If there were two stones in the middle, they were taken away and replaced by another stone on the next line.

And that’s it. Anyone was able to calculate in this way, but only to a limited extent. Regarding subtractions, you simply took away the number of stones that corresponded to the number you wanted to subtract. Of course, only as long as there still were stones left. The counting table did not know negative numbers. Multiplication worked perfectly since 3x3 is nothing else than 3+3+3. But if you wanted to know what 167x56 makes, it took quite a bit of work to find out. Dividing? Forget it. That was advanced mathematics and caused real problems to merchants.

The numbers used with the counting table were Latin numerals. They were perfectly adapted to the system. Let’s look at an example. This is how the year 2022 would look like in Latin script: MMXXII. I am sure you immediately understand which lines you have to put your stones on to express this number. Just put two on the M line (thousands), two on the X line (tens) and two on the I line (ones).

How to Calculate with Medieval Denominations

Those who calculated with coins only had to change the denominations of the individual lines. Correspondingly, the lowest line represented pennies, the middle line shillings and the top line pounds. Adjustments were simply made at a different rate, i.e. when 6 stones had accumulated on the penny line or 10 stones on the shilling line. For a merchant, the procedure was the same regardless of whether he added apples or money.

And Then Came Arabic Numerals

However, merchants often encountered practical problems in their daily lives by using the counting table. Imagine three merchants pooling their capital to equip a caravan. One gives 20, the second one 35 and the third one 49 guldens. And now you have to use the counting table to calculate how much of the profit of 218 guldens each of them is entitled to. A nightmare!

You can imagine how excited Italian long-distant merchants were when they first encountered Arabic numerals and written arithmetic in the Arab world. Modern numbers and the zero as a placeholder made a completely new form of addition and multiplication possible – provided one had memorized the multiplication table, which has been part of the syllabus ever since. Suddenly, division was possible too – there were negative results, fractions and, last but not least, it was possible to solve equations with one variable. By the way, all the mathematical signs such as +, -, = and the like that we take for granted today only developed in the Renaissance period when arithmetic with Arabic numerals experienced a real boom and the new system spread all over Europe.

The Lazy Human Being

The problem with the whole thing is that the new numbers favoured the decimal system. If you don’t believe me, try it yourself: Convert 48cm + 16cm + 23cm + 47cm into meters using written arithmetic. And now do the same with minutes. So, how many hours are 48 min + 16 min + 23 min + 47 min?

But the human being has no desire whatsoever to get used to new measures or units just because the old ones no longer fit the arithmetic system. In Western Europe, for example, a currency based on the decimal system was not introduced until about three centuries after the new way of calculating had established itself: the French Revolution forced its rational citizens to use a sensible monetary system. The fact that the human being likes to be unreasonable can be seen from how quickly many of the territories annexed by France, which were allowed to enjoy the pleasures of progress, returned to their gloriously unreasonable old monetary system. Britain, which has never been conquered by France, did not adopt the decimal system until 1971. 

And That’s Why the Barreme Was Needed

And that brings us to our little book, because livres, deniers and sous could not be multiplied by means of written arithmetic. And counting tables were no longer used either. Instead, a merchant would pull this little book out of his pocket whenever he wondered what he would have to pay if he didn’t buy exactly one pound of pepper but three quarters of a pound, five pounds or even 973 ½ pounds.

Thus, this small, unimportant-looking book, which we bought for 30 euros at the Heidelberg antiquarian bookshop Hatry, is a testimony to the transition from Roman to Arabic numerals and to the difficulty of mankind to adequately adapt to innovation.